| Numéro |
J. Phys. II France
Volume 2, Numéro 11, November 1992
|
|
|---|---|---|
| Page(s) | 2039 - 2063 | |
| DOI | https://doi.org/10.1051/jp2:1992250 | |
J. Phys. II France 2 (1992) 2039-2063
Structural study of the inverted cubic phases of di-dodecyl alkyl-
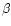 -D-glucopyranosyl-
rac-glycerol
-D-glucopyranosyl-
rac-glycerol
David C. Turner1, Zhen-Gang Wang2, Sol M. Gruner1, David A. Mannock3 and Ronald N. McElhaney3
1 Department of Physics, Joseph Henry Laboratories, Princeton University, Princeton, N.J. 08544, U.S.A.
2 Department of Chemical Engineering, 210-41 California Institute of Technology, Pasadena, Ca. 91125, Canada
3 Department of Biochemistry, Universtiy of Alberta, Edmonton, Alberta, Ca. T6G 2H7, Canada
(Received 3 June 1992, accepted in final form 2 July 1992)
Abstract
We present a quantitative study of the bicontinuous cubic phases in the didodecyl alkyl-
![]() -D-glucopyranosyl-rac-glycerol (rac-di-12:0
-D-glucopyranosyl-rac-glycerol (rac-di-12:0
![]() -GlcDAG) lipid-water system. A temperature-composition phase diagram determined using X-ray diffraction shows Ia3d and Pn3/Pn3m
cubic phase regions in addition to inverted hexagonal (H
-GlcDAG) lipid-water system. A temperature-composition phase diagram determined using X-ray diffraction shows Ia3d and Pn3/Pn3m
cubic phase regions in addition to inverted hexagonal (H
![]() ) and several lamellar phase regions. The diffraction data was used to determine the lattice repeat vector,
d, and, using suitable models, the lipid monolayer thickness,
) and several lamellar phase regions. The diffraction data was used to determine the lattice repeat vector,
d, and, using suitable models, the lipid monolayer thickness,
![]() , for all temperatures and compositions in the diagram. The models chosen for the cubic phases were based on lipid bilayers
straddling infinitely periodic minimal surfaces (IPMS) as described previously in the literature [1]. Using the structural
data derived from the phase diagram, the lyotropic phase transition between the two cubics was modeled by a simple curvature
free energy theory. A new result of this theory was an estimate for the Gaussian curvature bending modulus of the lipid monolayer.
The model was found to quantitatively describe the phase transition, particularly for phase behavior at low hydration. Our
model suggests some universal features should be present in any system that shows non-lamellar phases and we discuss those
features with respect to the phase diagrams available in the literature.
, for all temperatures and compositions in the diagram. The models chosen for the cubic phases were based on lipid bilayers
straddling infinitely periodic minimal surfaces (IPMS) as described previously in the literature [1]. Using the structural
data derived from the phase diagram, the lyotropic phase transition between the two cubics was modeled by a simple curvature
free energy theory. A new result of this theory was an estimate for the Gaussian curvature bending modulus of the lipid monolayer.
The model was found to quantitatively describe the phase transition, particularly for phase behavior at low hydration. Our
model suggests some universal features should be present in any system that shows non-lamellar phases and we discuss those
features with respect to the phase diagrams available in the literature.
61.30E - 64.70M
© Les Editions de Physique 1992



